|
Коллоквиум 2 [информатика]
|
|
| ldo2 | Дата: Пятница, 16.11.2007, 22:10 | Сообщение # 1 |
 Сержант
Группа: 11
Сообщений: 88
Статус: Offline
| Вот уже есть программы без решений, как мы потом поймем что больше половины или все из них не правильные.
И самое главное, запомните НИКОГДА ТАК НЕ ДЕЛАЙТЕ!!!(тем более на коллоквиуме)
программы PS давайте создадим страницу на википедии с решениями ко второму коллоквиуму, чтобы каждый мог править (даже Роганов;)
Основная проблема современности - коммуникационная.
jabber: ldo2@jabber.ru
skype: ldo1
|
| |
| |
| kmeaw | Дата: Пятница, 16.11.2007, 23:21 | Сообщение # 2 |
 Рядовой
Группа: Проверенные
Сообщений: 35
Статус: Offline
| http://kmeaw.com/files.tar.gz - это я когда-то писал, что это и как работает - не помню
--
kmeaw aka bdd1
|
| |
| |
| ldo2 | Дата: Суббота, 17.11.2007, 20:08 | Сообщение # 3 |
 Сержант
Группа: 11
Сообщений: 88
Статус: Offline
| плохое начало, но будем рассчитывать на хороший конец:)
Коллоквиум2
Исходники PS извините за форматирование
Основная проблема современности - коммуникационная.
jabber: ldo2@jabber.ru
skype: ldo1
|
| |
| |
| Chuvaver | Дата: Суббота, 24.11.2007, 21:21 | Сообщение # 4 |
 Сержант
Группа: 11
Сообщений: 54
Статус: Offline
| Функция МакКарти (если кому интересна...)
МакКартиДобавлено (24.11.2007, 21:21)
---------------------------------------------
Еще кое-что
Собираю монеты! Приму в дар, все что не жалко!!!
|
| |
| |
| Twilight_Summoner | Дата: Среда, 28.11.2007, 20:28 | Сообщение # 5 |
 Рядовой
Группа: Заблокированные
Сообщений: 37
Статус: Offline
| Code #1
def M(n)
n > 100 ? n-10 : M(M(n+11))
end
puts M(gets.to_i)
#2
def C(n, k)
(k == 0 || k == n) ? 1 : C(n-1, k) + C(n-1, k-1)
end
puts C(gets.to_i, gets.to_i)
#3
def A(m, n)
(m==0) ? n + 1 : (n == 0) ? A(m - 1, 1) : !(m-1, A(m, n - 1))
end
puts A(gets.to_i, gets.to_i)
#4
print "a->"
a = gets.to_i
print "b->"
b = gets.to_i
x, y, z = a, b, 1
while y > 0
if y % 2 == 0
y, x = y/2, x*x
end
end
#5
print "n->"
n = gets.to_i
a, b = 0, n + 1
while a + 1 != b
c = (a + b) / 2
if c*c <= n
a = c
else
b = c
end
end
puts "sqrt(#{n}) = #{a}"
#6
b = [1, 6, 3, 7, 2, 7, 8, 1, 7, 6, 2, 0]
i = b.size - 1
x = 8
i -= 1 while x != b[i]
puts "Element #{i} = #{b[i]}"
Остальные куда-то подевались, хотя я их вроде все выгребал...
Разгильдяй, пофигист по жизни, весельчак)
|
| |
| |
| Chuvaver | Дата: Среда, 28.11.2007, 20:32 | Сообщение # 6 |
 Сержант
Группа: 11
Сообщений: 54
Статус: Offline
| kmeaw, может хоть ты объяснишь тупым студентам-первокурсникам, как доказывать правильность рекурсивных программ с 2 переменными?
Собираю монеты! Приму в дар, все что не жалко!!!
|
| |
| |
| ldo2 | Дата: Среда, 28.11.2007, 21:52 | Сообщение # 7 |
 Сержант
Группа: 11
Сообщений: 88
Статус: Offline
| Еще одна попытка что-то решить
Возможно там что-то не правильно ))
Сами проверяйте гы(((
Основная проблема современности - коммуникационная.
jabber: ldo2@jabber.ru
skype: ldo1
|
| |
| |
| Chuvaver | Дата: Среда, 28.11.2007, 22:51 | Сообщение # 8 |
 Сержант
Группа: 11
Сообщений: 54
Статус: Offline
| kmeaw, мне хочется знать, например, что делать с функцией Аккермана, то есть с доказательством рекурсивной программы на правильность, написанной но ней (то что она закончится вроде понятно)
Собираю монеты! Приму в дар, все что не жалко!!!
|
| |
| |
| kmeaw | Дата: Четверг, 29.11.2007, 00:00 | Сообщение # 9 |
 Рядовой
Группа: Проверенные
Сообщений: 35
Статус: Offline
| Chuvaver, т.е. тебе нужно доказать, что эта функция возвращает то же самое значение, которое дано в определении?
--
kmeaw aka bdd1
|
| |
| |
| Chuvaver | Дата: Четверг, 29.11.2007, 09:08 | Сообщение # 10 |
 Сержант
Группа: 11
Сообщений: 54
Статус: Offline
| kmeaw, да, именно это..
Собираю монеты! Приму в дар, все что не жалко!!!
|
| |
| |
| kmeaw | Дата: Четверг, 29.11.2007, 21:50 | Сообщение # 11 |
 Рядовой
Группа: Проверенные
Сообщений: 35
Статус: Offline
| Определение.
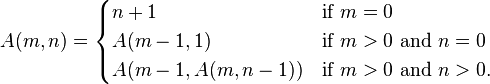 Code
# Неоптимизированный код
def a(m,n)
if m == 0
n + 1
elsif n == 0
a(m-1, 1)
else
a(m-1,a(m,n-1))
end
end
Рассмотрим три случая:
- 1. m = 0;
Тогда программа немедленно завершает работу и возвращает n+1, что соответствует определению;
- 2. n = 0;
Тогда программа будет выполнять a(m-1,1). Если m = 1, то получим состояние (1), для которого доказана правильность. Иначе получим состояние (3), правильность которого докажем ниже. Пока что будем считать его доказанным.
- 3. m > 0, n > 0.
Тогда программа будет выполнять a(m-1, a(m,n-1)). Рассмотри a(m,n-1). Если n = 1, то получим случай (2), который уже доказан. Иначе опять получим случай (3). Несложно показать, что domain(A) => A>0 (докажите это сами). Значит, a(m-1, a(m,n-1)) переходит к случаю (1), если m = 1. Иначе, опять получим случай (3).
Картинка:
 Программа завершает работу, т.к. при каждом переходе в другое состояние меняется хотя бы один аргумент (m или n) в сторону уменьшения. Таким образом, за конечное время (число переходов) получим m = 0 или n = 0. Программа работает правильно, т.к. аналогичные рассуждения можно провести для определения данной функции.
--
kmeaw aka bdd1
|
| |
| |












